Articles
How to Create Autoregressive Integrated Moving Average (ARIMA) Models
- By Bryan Lapidus, FP&A
- Published: 2/6/2019
Statistical tools are gaining in importance as the volume, variety, and velocity of data increases. But are we using the tools built into statistical software the right way? Do we fully understand their potential? Are we even using them at all? Here is how to create an autoregressive integrated moving average (ARIMA) model.
WHAT IS ARIMA?
ARIMA, or autoregressive integrated moving average, is a predictive time-series modeling approach that looks to fit data that’s provided on a periodic basis. ARIMA regresses past data for forecasts, but does not require advanced statistical knowledge to build, can be built using minimal data, and can be quickly developed, implemented and tested.
WHAT IS A USE CASE FOR ARIMA?
Here is an example:
A mid-market retailer wanted a more reliable approach to forecasting sales for the upcoming six months to better understand, predict, and manage the volatility and fluctuations they experience month to month. Cadilus Inc., a firm that provides FP&A services, assembled 10 years of daily sales from the client, restructured the incoming data, and built a modeling capability to predict sales on a six-month forward-looking basis.
The Cadilus team utilized R packages to complete the project. They kicked off the process by prepping the data for time-series analysis and examining it for significant outliers that could potentially affect model fitting. The team then decomposed the data into the appropriate components: season, trend, cycle (and the residuals). Once those components were determined, the team ran formal statistical tests to determine stationarity, assuring that the series fluctuates in a consistent pattern—a key requirement for ARIMA modeling. Once stationarity was determined and addressed, the team evaluated the order of parameters (given the components) for the model. Additional evaluations were completed for correlations, autocorrelations and order parameters.
The model was fitted, improved over a few iterations, and the final predictions were made for the upcoming six months. Graphical illustration of forecast is below:
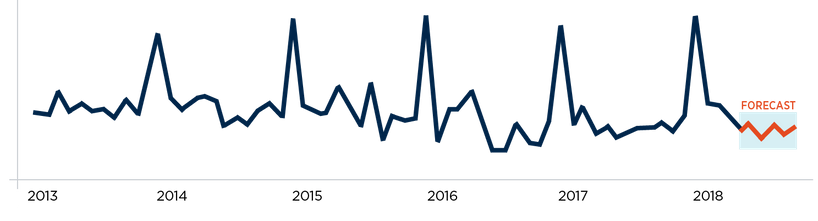
When comparing the monthly actuals to the predicted values, they fell within the prediction range, said Dan Shin of Cadilus. This allowed the client to feel comfortable that the monthly variations they were experiencing were likely due to seasonal and cyclical components versus unique events.
Learn more about the importance of creating autoregressive integrated moving average (ARIMA) models here.
Want to learn more about business statistics?Join your FP&A peers at FinNext 2019 to be part of the future of finance.Copyright © 2024 Association for Financial Professionals, Inc.
All rights reserved.

